話を次に進める前に、少し寄り道して計算が便利になるクラスを紹介しておきます。 変数aの平方根、サイン、コサイン、座標計算……。非常に面倒な計算を簡単に行う事が出来るクラス、 それが今回紹介するMathクラスです。
Mathクラスに関して、公式リファレンス内で詳細は省かれているようなので、ここで補足説明をしておきましょう。
尚、この回に関しては読み飛ばしても構いません。必要になったら戻ってきてくださいね。
数学関数Mathの使い方
ここからは、吉里吉里/TJSに用意されているクラス(設計図)を使いながら、新しい機能の紹介をしていきます。 前提としてクラスの使い方が分かっている事が求められるので、 よく分からない方はクラスの項目を読み直してみてください。
今後もTJS2リファレンスを読みながら進めて頂ければ、より分かりやすくなります。 せっかく、開発者であるW.Dee 氏自らが作成された優秀なリファレンスがあるので、蛇足はしません。
Mathクラスはメンバー変数を持ちません。(持っていたとしても、参照されるべきではありません。) ですから、参照するのはメンバー関数とメンバープロパティのみです。 そして、Mathクラスは実物を作る必要がありませんので、次のように参照します。
Math.メンバー
例えば、円周率(パイ)を参照するには次のように書きます。
Math.PI
※PIは円周率を指すMathクラスのメンバープロパティです。
ところで、この書き方は不思議だと思いませんか? これまで、クラスというと単なる設計図なので実物を作りなさい、と説明してきました。 ところが、今回は実物を作る事無く、設計図自体を参照しています。
実は設計図(クラス)のメンバー自体を参照する事は可能なんです。 例えば System.inform() のように、Systemクラスの実物を作る事無く、 Systemクラスのメンバー自体を参照してきましたね。 次のプログラムも正常に動く事が確認できます。
class print { function show(msg) { System.inform(msg); } } print.show("こんにちは!");
実物(オブジェクト)ではなく、クラスのメンバー自体を参照出来る。 これは後で重要になるので、覚えておいてくださいね。
この仕組みを利用すると、System.informの別名関数を簡単に作る事が出来ます。
var print = System.inform;
print("こんにちは!");
以前に説明したクロージャという機能と、クラスのメンバーの参照という方法を使っています。
ランダムに数を返す
ゲームではランダムな数(乱数)を必要とする場面が多くあります。 例えば、RPGである武器を持っていると3~5回攻撃できる武器。 カードゲームで、山札から1~3枚カードを引ける…といった具合です。
- 0以上n以下の数を求める方法
- min以上max以下の数を求める方法
ここでは、この二点を紹介します。
0~nの数を返す公式
まず、ランダムな数を取得するために、random関数を使います。 この関数は0以上1未満…つまり、0~0.999999…の値を返します。
Math.random()
0以上1未満の数を返すのだから、単純にnを掛ければ0以上n未満の数が取得できますね。 取得した数は実数ですから、intを使って整数にします。
int(Math.random() * n)
1を掛けると、intによる小数点切捨てで必ず0しか返って来ません。(1未満の数しか返さないからですね。) 2を掛けると、Math.random()が0.5以上の値を返した時に1になります。 同じく、2を掛けただけでは最高値は1.99999...なので2は超えません。
同様に考えると、3を掛けるとMath.random()が0.667..以上を返した時に2になります。そして3を超えない。
この事実から、Math.random()にnを掛けると、0以上n未満の数を返す事が確認できます。
という事は、n以下の数を返して欲しい場合、nに1を上乗せすれば良い事になります。
int(Math.random() * (n+1))
これで0以上n以下の数を求める公式の完成です。
最小値~最大値の数を返す公式
0以上n以下の数を取得するのに、次のように書きました。
int(Math.random() * (n+1))
この(n+1)の部分のnは希望数の最大値を指します。最小値は0ですね。 ここで、最小値を1にしたい場合、返された数に1を加算すれば、0を返される事はなくなりますね。
int(Math.random() * (n+1)) + 1
ただし、このままでは1~nの数が返ります。 Math.random() * (n+1)によって0~nが返されるからです。 ですから、nの数から最小値を考慮して、減算する必要があります。
int(Math.random() * (n-1+1)) + 1
※単純にnの値から最小値を減算し、最後に最小値を加算します。
これで1以上n以下の数を返す公式が出来上がりました。 わかり易くするために、最大値をMAX、最小値をMINとしてまとめます。
int(Math.random() * (MAX-MIN+1)) + MIN
必要であれば、これを関数として保存しておけば、任意の数の乱数を導き出すことが可能です。
数学が嫌いな方にとっては、分かりづらいかもしれません。 ただ、公式の意味を理解する必要はありません。 本質さえ分かっていれば、それで十分なのです。
三角関数
正弦、余弦、正接を計算する関数です。 「サイン」「コサイン」「タンジェント」という呼び方の方が分かりやすいでしょうか。 プログラムでは、シューティングゲーム等の角度計算に多く用いられています。
Math.sin(rad)…角度radの正弦
Math.cos(rad)…角度radの余弦
Math.tan(rad)…角度radの正接
radはラジアンという角度の単位を使用します。 よって、0~360という数値を指定しても、正しい結果は得られません。
角度ラジアンについて
TJSでは0~360度という角度を用いず、ラジアンという単位を利用します。 よって、正弦や余弦を計算する場合、角度はラジアンで指定する必要があります。
180度はラジアンのパイである事から、以下の式でラジアンに変換できます。
角度r * (2 * Math.PI / 360)
例えば、サイン90度は1ですが、ラジアンへ変換しないと値が狂います。
Math.sin(90)……0.89399...?
ラジアンを指定すると、1と表示されます。
Math.sin(90 * (2 * Math.PI / 360))
また、逆三角関数も扱えます。
Math.asin(rad)…角度radの逆正弦
Math.acos(rad)…角度radの逆余弦
Math.atan(rad)…角度radの逆正接
ラジアン変換を頻繁に行うのは面倒な事ですので、 次のような汎用関数を作っておく事をお勧めします。
function getRadian(x) { return x * (2 * Math.PI / 360); }
2数の逆正接
アクションゲーム等では、敵は自分をめがけて突進してきたり、 ちゃんとこちらを向いて、正確な角度で弾を発射してきます。不思議ですねぇ。 今回は、ある座標を基点として、ある座標への角度を出す関数を紹介します。
まずは、以下の図をご覧ください。

このx軸を基点として、座標x,yまでの角度pを計算したい場合、以下の関数が使えます。
Math.atan2(y, x)
数学的に言うと、直交座標を極座標へ変換を行ってくれます。
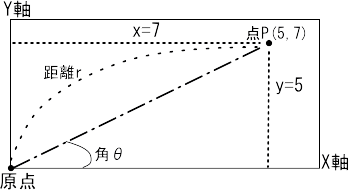
直交座標とは、点Pを原点からの縦横の距離で表すものです。x=7,y=5である場合、点Pは(7,5)と表現できます。
極座標とは、原点から点Pまでの距離と、x軸を基点とした点Pへの角度で、点Pを表すものです。atan2はこの角度を計算出来ます。
※角度が分かれば距離が分かりますし、xy座標が分かれば角度が分かる…という三角比の考え方を利用したものですね。
※xy座標の引数の順番に注意。最初にy座標、次がx座標です。順番を間違えることが多いので注意しましょう。
例えば、味方のオブジェクトをmy、敵をemyとした場合、 各座標をxyを減算してatan2に与えてあげれば、双方の角度を求める事が可能です。 (どちらを原点にするかによって、減算される側は変わりますので注意してください。)
Math.atan2((my.y - emy.y) , (my.x - emy.x)
本ページでは、実際の利用法については割愛させていただきます。 あまり細かく説明すると入門では無くなってしまいますし、 プログラムとは別の話になってしまうからです。
- ラジアン値を(2*Math.PI/360)で割れば、0~360度といった角度に戻せます。
- atan2で得られた角度を元に、正弦と余弦を計算すれば、 原点から座標までの横の距離と縦の距離が導き出せます。 これを使えば、味方を直接狙う弾という実装が可能です。
- 自分を中心として円形に弾を出すには「r = 360度/弾数」を基本角度として、for文等で回します。 例えば、Zという変数にrを加算しつつ正弦と余弦を計算すれば、 「全弾の角度」と「縦と横の移動距離」が導き出せます。
その他のメンバー
公式リファレンスでは数学関数の詳細が書かれていませんので、 その他のメンバー関数とメンバープロパティについて補足しておきます。 ※よく使われそうなものに留めます。
| abs(x) | xの絶対値を返します。絶対値とは、簡単に言えば符号を取り除いた数値です。Math.abs(-0.33)なら0.33を返します。 |
|---|---|
| round(x) | xを四捨五入した数を返す。Math.round(0.4)は0.0、Math.round(1.5)は2です。 |
| max(num1,num2) min(num1,num2) | maxは二数の大きいほう、minは小さい方を返します。 max(1,2)は2を、min(100,20)は20を返します。(もちろん、通常は値の判別が出来ない変数を引数にします。) |
| PI | 円周率を指します。円の面積を求める場合など、3.14を掛けるよりもPIを利用する方が精度が高くなります。 例) 2 * Math.PI * r (rは半径) |